-
-
-
-
들어가며
-
-
컴퓨터 비전의 하위 도메인인 3D Reconstruction, Novel-View-Synthesis 을 공부하다보면 Volume Rendering, 혹은 그와 유사한 개념을 자주 접하게 된다.
-
-
하지만 렌더링에 사용되는 여러 개념을 혼동하거나 제대로 이해하지 못하는 경우가 많다.
-
-
특히 Splatting이 정확히 무엇인지에 대해서는 명쾌하게 답해주는 자료를 찾기 어려웠다.
-
-
각 개념을 이해해야 이후 Splatting, Ray Casting, 3D Gaussian splatting, NeRF 등에 잘 대응할 수 있으니 헷갈리는 부분을 짚고 넘어가려 한다.
-
-
이 글은 최초의 Splatting method 저자 Lee Alan Westover의 논문 "Alan, Lee. "SPLATTING: A Parallel, Feed-Forward Volume Rendering Algorithm." (1991)."를 참고했다.
-
-
Volume Rendering (볼륨 렌더링)
-
-
Surface Rendering (표면 렌더링)
-
-
Clipping (클리핑)
-
그렇다면 볼륨 렌더링을 구현하는 방법들에는 무엇이 있을까?
-
Object-order technique
-
즉 Splatting 이란 볼륨 렌더링 구현 방법 중, Object-order technique 방법에 속하는 알고리즘이다. (Proposed by Lee Westover, 1990)
-
그렇다면 Splatting 이란 정확히 무엇인가?
-
-
Splatting 은 각 샘플이 공간의 많은 점, 즉 이미지 평면의 많은 픽셀에 어떻게 기여할 수 있는지를 분포 함수의 관점에서 고려하는 알고리즘이다.
-
우선 Splatting 의 주요 개념과 단계를 알아보자.
-
바로 이해하기 어려우므로 배경 개념부터 천천히 이해해보자.
-
이제 3D 커널과 그것의 2D 스플랫이 어떻게 작동하는지 알아보자.
-
이제 Splatting 알고리즘 개요를 알아보자.
-
복셀의 이미지 평면에 대한 기여
-
Footprint function
-
Footprint Table
-
Footprint Table 의 사용
-
색상 할당

# 모바일에서 수식이 깨져보이니 PC모드 활용을 권장드립니다.
들어가며
컴퓨터 비전의 하위 도메인인 3D Reconstruction, Novel-View-Synthesis 을 공부하다보면 Volume Rendering, 혹은 그와 유사한 개념을 자주 접하게 된다.
하지만 렌더링에 사용되는 여러 개념을 혼동하거나 제대로 이해하지 못하는 경우가 많다.
특히 Splatting이 정확히 무엇인지에 대해서는 명쾌하게 답해주는 자료를 찾기 어려웠다.
각 개념을 이해해야 이후 Splatting, Ray Casting, 3D Gaussian splatting, NeRF 등에 잘 대응할 수 있으니 헷갈리는 부분을 짚고 넘어가려 한다.
이 글은 최초의 Splatting method 저자 Lee Alan Westover의 논문 "Alan, Lee. "SPLATTING: A Parallel, Feed-Forward Volume Rendering Algorithm." (1991)."를 참고했다.
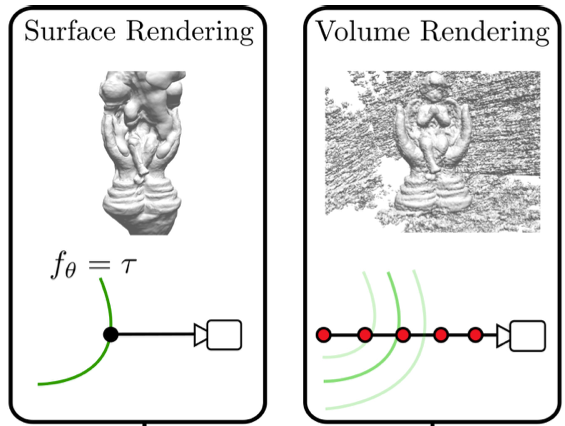
Volume Rendering (볼륨 렌더링)
- 3D Volumetric data에서 직접 2D 이미지를 생성하는 기술
- 전체 3D 데이터를 2D 이미지로 매핑 함.
- 3D 데이터 내의 각 지점(복셀)에 대한 색상과 불투명도를 결정하여, 최종적으로 2D 이미지에 표현되는 시각적 효과를 결정
- 알고리즘 복잡성이 높고 시간이 오래 걸리지만 전체 정보를 유지함.
- 구름, 안개와 같은 비정형적 현상의 렌더링에 유리함.
- 2020년 ECCV에서 발표된 NeRF(Neural Radiance Fields)는 볼륨 렌더링을 미분가능한 방식으로 확장함.
Surface Rendering (표면 렌더링)
- 기하학적 기본 요소를 사용해 볼륨 데이터에 포함된 표면의 이미지를 생성하는 기술
- 기하학적 기본 형태는 주로 삼각형 또는 점이다.
- 볼륨 렌더링과는 다르게 표면에만 집중한다.
- 볼륨 데이터 내부의 구조보단 표면의 상세한 구조와 형태에 집중.
Clipping (클리핑)
- 렌더링 과정 중 볼륨의 일부를 제거하여 나머지 부분을 표시하는 과정.
- 불필요한 부분을 제거해 렌더링 효율성을 높일 수 있음.
- 볼륨 또는 표면 렌더링에 사용 가능함.
그렇다면 볼륨 렌더링을 구현하는 방법들에는 무엇이 있을까?
Object-order technique
- 볼륨 데이터가 이미지 평면에 매핑되는 포워드 매핑 체계를 사용함.
- -> Splatting (관련 논문: 3D Gaussian Splatting for Real-Time Radiance Field Rendering)
Image-order technique
- 이미지 평면의 각 픽셀에서 볼륨 데이터를 통해 광선을 캐스팅하여 픽셀 값을 결정하는 백워드 매핑 방식을 사용함.
- -> Volume Buffer, Ray Casting (관련 논문: Representing Scenes as Neural Radiance Fields for View Synthesis)
Hybrid technique
- 위의 두 방법을 융합
- -> Cell-by-cell V-buffer, Shear-warp
모든 방법들의 목표는 같다. 이미지를 만들어 내는 것이다.
즉 Splatting 이란 볼륨 렌더링 구현 방법 중, Object-order technique 방법에 속하는 알고리즘이다. (Proposed by Lee Westover, 1990)
그렇다면 Splatting 이란 정확히 무엇인가?
Splatting 은 각 샘플이 공간의 많은 점, 즉 이미지 평면의 많은 픽셀에 어떻게 기여할 수 있는지를 분포 함수의 관점에서 고려하는 알고리즘이다.
우선 Splatting 의 주요 개념과 단계를 알아보자.
- 에너지 분산(Distributing Energy): 입력 샘플들로부터 에너지를 공간에 분산시킴. 이는 각 샘플이 가지고 있는 정보(예: 밝기, 색상)를 공간의 여러 지점에 전달하는 과정을 의미함..
- 이미지 평면 발자국 계산(Calculating Image Plane Footprint): 각 데이터 샘플에 대한 '풋프린트' (Footprint)를 이미지 평면에서 계산함. 풋프린트는 해당 샘플이 이미지 평면에 어떻게 투영되는지를 나타내는 영역으로, 샘플의 에너지가 이미지 평면에 어떻게 분포될지를 결정함.
- 샘플의 에너지 분포(Spreading the Sample's Energy): 계산된 풋프린트를 사용하여 각 샘플의 에너지를 이미지 평면에 분산시킴. 이 과정에서 한 샘플이 이미지의 여러 픽셀에 영향을 줄 수 있으며, 이는 부드럽고 연속적인 시각적 효과를 생성함.
바로 이해하기 어려우므로 배경 개념부터 천천히 이해해보자.
우선 픽셀을 샤프한 테두리를 가진 정사각형이 아닌, 아래 이미지처럼 흐릿한 경계를 가진 원형의 빛이라고 생각해보자.

Splatting 에서, 복셀도 같은 방식으로 여겨진다.
Descrete point 가 아닌, 가우시안 분포를 나타내는 흐릿한 구형으로 말이다.
(이 3D 가우시간은 'Reconstruction Kernel' 로 불린다.)
따라서 우리는 볼륨을 불연속적인 물체가 아닌 연속적인 함수(Gaussians)의 집합으로 정의되는 연속적인 물체로 생각할 수 있다.
그리고 각 가우시안의 중심에 복셀의 밀도를 지정한다.
중심에서 멀어질 수록 밀도는 가우시안 분포에 의해 빠르게 떨어진다.
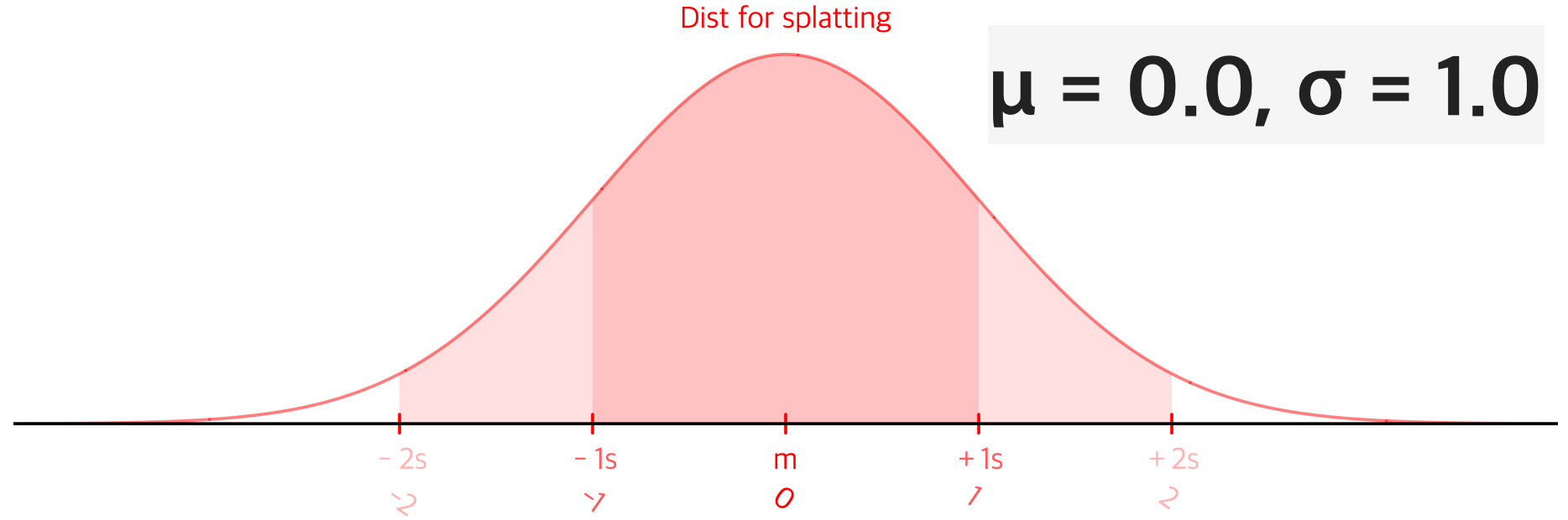
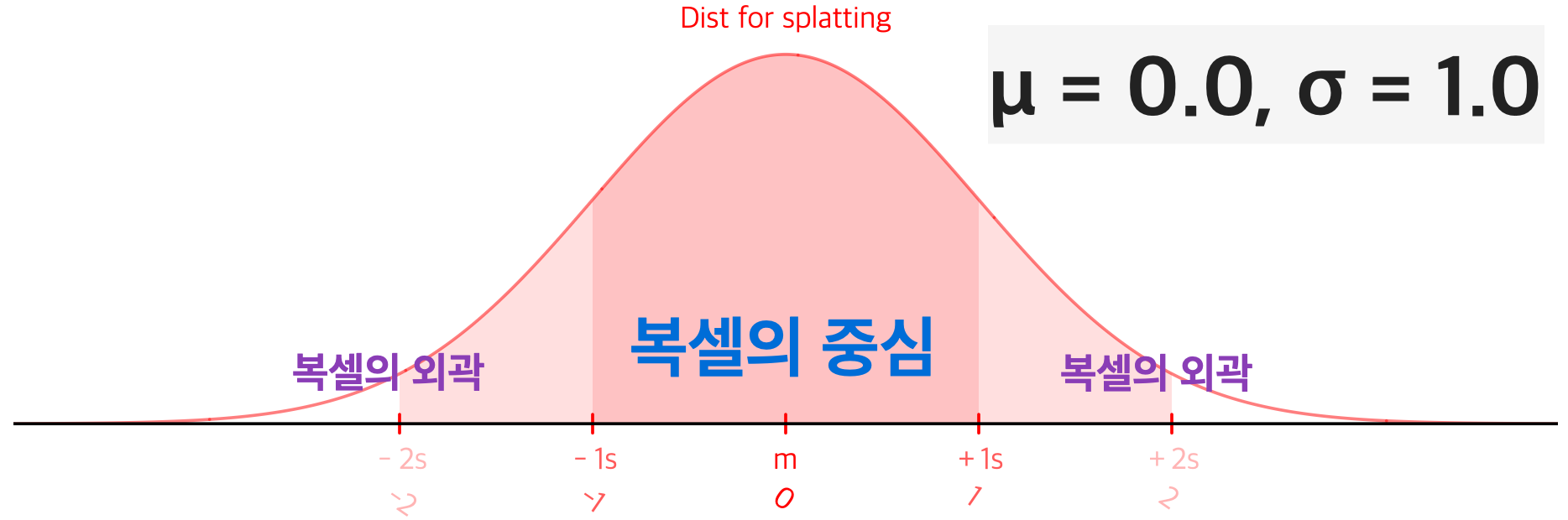
일반적으로 μ = 0.0, σ = 1.0, 피크값=1.0 을 사용하며 반경 2.0 바깥의 값은 잘라낸다. 즉 그 바깥 영역의 밀도는 0이다.
(물론 위와 같은 표준 정규분포에서 피크값이 1.0이 나올 순 없다. 시각적 표현을 위해 조정한 분포를 사용한다.)
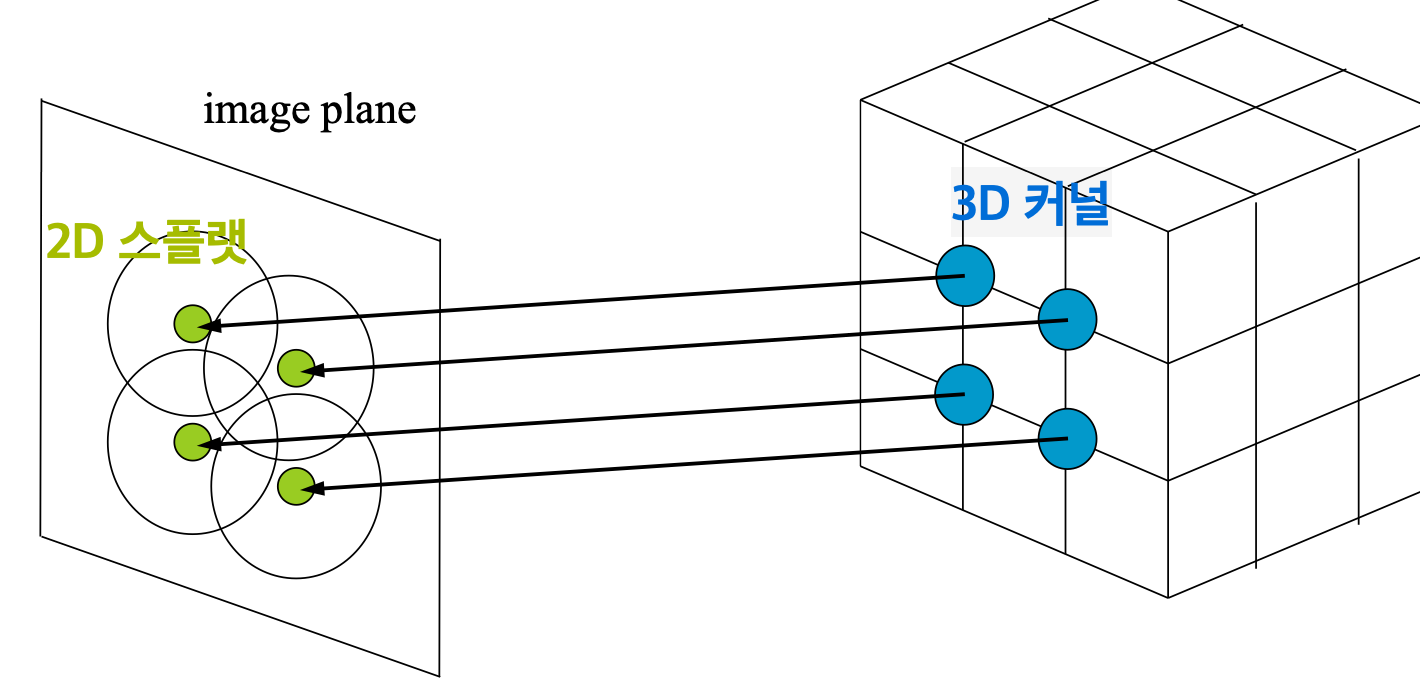
이제 3D 커널과 그것의 2D 스플랫이 어떻게 작동하는지 알아보자.
3D 커널과 2D 스플랫은 서로 오버랩된다.
앞서 말했듯, 3D 커널은 볼륨 데이터 내의 각 점(복셀) 주위에 분포하는 값을 정의하는 함수다. 2D 스플랫은 이 커널이 2차원 이미지 평면에 투영되었을 때의 형태다. 이 스플랫들은 서로 오버랩되어 이미지 평면에 분포한다.
스플랫들이 오버랩되는 것이 중요한 이유는 그렇게 함으로써 다양한 카메라 포즈가 달라지거나 줌인/줌아웃(스케일링)을 하더라도 일관되며 연속적이고 부드러운 이미지를 볼 수 있기 때문이다.
*카메라의 줌인/줌아웃 시 2D 스플랫은 시각적 일관성을 위해 크기가 조절된다.
이제 Splatting 알고리즘 개요를 알아보자.
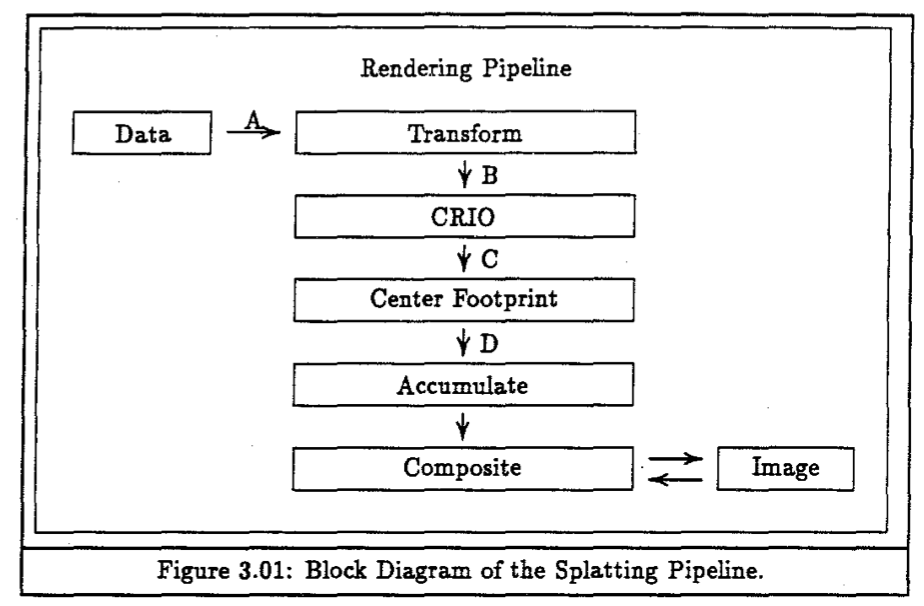
알고리즘은 변환, 음영, 재구성, 가시성 처리를 통해 최종 2D 이미지를 제작한다.
3D 볼륨 데이터는 복셀의 격자로 구성되어 있다.
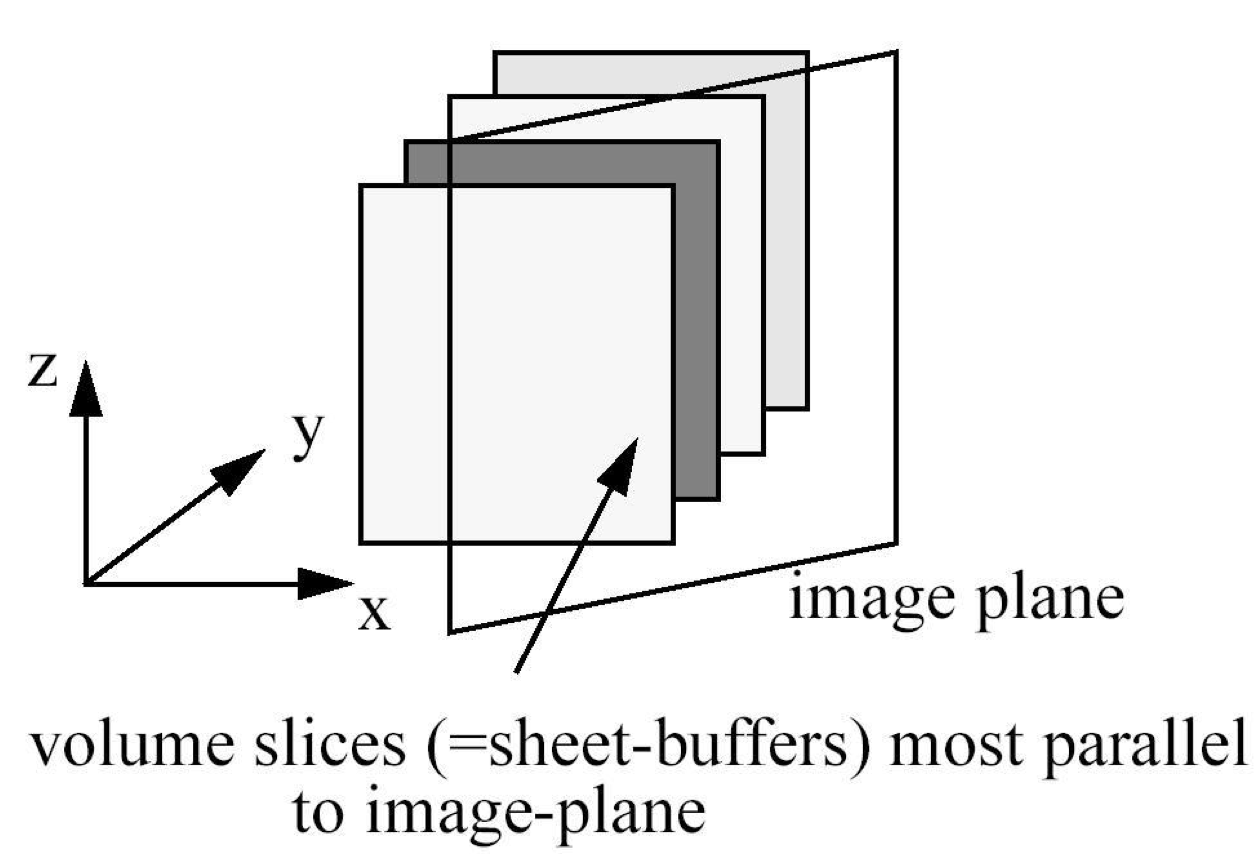
1. 알고리즘은 볼륨을 Sheet(시트) 라고 불리는 한 겹씩 순차적으로 처리한다. 이때, 시트는 복셀의 층을 의미한다.
2. 처리할 시트를 선택할 때, 이미지 평면과 가장 평행한 시트(x-y, x-z, y-z)를 선택한다. (렌더링 효율성을 위해)
3. 선택한 시트의 각 복셀은 (i, j, k) 그리드 공간에서 (x, y, z) 스크린 공간으로 변환된다.
이 변환에는 translation, rotation이 동반될 수 있다.
이 과정에서 3D -> 2D 평면 매핑이 이뤄진다.
4. 변환된 각 복셀은 색상(RGB)와 투명도(alpha)를 갖도록 음영처리된다. (Shaded)
여기서 Shading rule이 사용된다. <x,y,z,R,G,B,A>.
여기서 가시성(Visibility) 처리가 이뤄진다.
5. 누적 시트에 대한 복셀의 영향 결정 (재구성 단계)
각 복셀이 누적 시트(Accumulation sheet)에 어떤 영향을 미칠지 결정한다.
이는 각 복셀을 누적 시트에 projection하는 과정을 통해 이뤄진다.
이를 위해 풋프린트 함수 (footprint function)을 정의하고 계산된다.
데이터 샘플은 재구성 커널(reconstruction kernel)과 합성되어(data sample이 convolved with), 이 샘플의 이미지를 생성한다.
-> 앞에 설명한 3D 가우시안이 재구성 커널임. 3D 가우시안, 재구성 커널은 복셀의 데이터값을 주변 공간에 어떻게 확산시킬지를 정의하는 함수이다.
6. 시트처리 후 누적 시트와 작업 이미지의 결합 (가시성 처리)
한 시트의 모든 복셀이 처리되면, 누적 시트는 중간 단계의 작업 이미지와 결합된다.
이 과정에서 합성 연산자(Composition operator)를 사용함.
7. 모든 시트 처리 후 최종 이미지 생성
복셀의 이미지 평면에 대한 기여
1. 투영된 3D 가우시안 커널의 2D 영역
3D 공간에서 정의된 가우시안 커널 (함수)이 2D 이미지 평면에 투영될 때의 영역을 '스플랫' 혹은 '풋프린트'라 한다.
2. 데이터셋을 연속 함수로 생각하기
데이터셋은 부드러운 가우시안 커널 (함수)에 의해 조각별로 정의된 연속함수로 정의된다. 각 복셀은 이 연속함수의 일부를 형성한다.
3. 볼륨에 대한 복셀의 기여 (Contribute)
볼륨에 대한 복셀의 기여는 다음과 같은 식으로 표현된다.
$$ contribution_s(x,y,z) = h_v(x-x_s, y-y_s, z-z_s)\rho (s) $$
여기서, $ h_v $ 는 볼류메트릭 재구성 커널이고, $ \rho (s) $ 는 복셀의 밀도를 나타낸다.
즉, 복셀의 밀도가 클 수록 볼륨 더 많은 기여를 한다. (NeRF의 opacity를 떠올리게 함.)
이처럼 복셀의 데이터값이 주변 공간에 확산되는 과정은 재구성 커널과 복셀 밀도의 곱으로 계산된다.
이를 다시 말해 '볼륨에 대한 복셀의 기여'라고 한다.
참고로, 복셀의 밀도 $ \rho (s) $ 는 $ \rho (s) = \rho (x_s, y_s, z_s) $ 로 정의된다.
4. 이미지 평면 픽셀에 대한 복셀의 기여 (Contribute)
복셀 데이터 샘플 $ s $ 가 이미지 평면 픽셀 $ p \to (x, y) $ 에 미치는 기여는 아래 식으로 표현된다.
$$ I_s(p) = I_s(x, y) = \rho (s)\int_{-\infty }^{\infty}h_v(x-x_s, y-y_s, w)dw $$
여기서 $ w $ 는 스크린에 수직인 광선 (네거티브 z축, pointing into the screen)을 따라 계산되며 그 원점은 $ (x, y) $ 이다.
또한 주어진 복셀에 대해, $ \rho (s) $ 는 $ \rho $ 가 w에 독립적이므로 일정하다.
때문에, 밀도항을 적분 밖으로 옮길 수 있다.
다시 한 번, 적분은 복셀의 밀도에 독립적이라는 점에 유의해야 한다.
5. $ x_s, y_s, z_s $
복셀의 위치를 나타내는 3차원 공간 상의 좌표
6. $ x, y, z $
카메라 기준의 3차원 공간 상의 좌표. 즉 볼륨 데이터가 projection 되어야 하는 이미지 평면의 위치를 나타냄.
7. 재구성 커널 h의 의미
$$ h_v(x-x_s, y-y_s, z-z_s) $$
이 커널(함수)는 중심점에서 멀어질수록 값이 감소하는 형태를 갖는다.
복셀의 3차원 상 좌표 $ x_s, y_s, z_s $ 에서 이미지 평면 상의 관찰점 $ x, y, z $ 까지의 거리에 따라 복셀이 갖는 영향력을 나타내는 것이다.
즉 복셀의 중심으로부터 멀어질수록 영향력은 감소하며, 이를 통해 볼륨 데이터의 부드러운 그라데이션을 확보한다.

위 그림처럼 복셀의 중심은 해당 복셀이 가진 데이터 값(예: 밀도, 색상)의 영향을 가장 강하게 받기 때문이다.
따라서 결과값은 입력값의 가중평균이다.
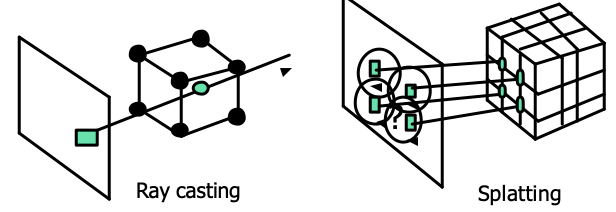
여기서 포워드 매핑 vs. 백워드 매핑의 차이가 드러난다.
포워드 매핑 (Splatting)
- 포워드 매핑 방식에서의 컨볼루션은 입력이 출력에 에너지를 분배하여 출력을 생성하는 것으로 본다.
- 여기서 스플래팅 방식은 각 입력 포인트(복셀)가 이미지 평면의 여러 픽셀에 영향을 미치는 것을 의미한다
- 즉, 하나의 입력이 여러 출력 픽셀에 '에너지'를 분배함으로써 최종 이미지가 형성된다.
백워드 매핑 (Ray Casting)
- 백워드 매핑 방식에서의 컨볼루션은 출력을 입력의 가중 평균으로 생성하는 것으로 간주한다.
- 즉, 각 입력 포인트(예: 복셀)의 기여도가 가중치에 따라 계산되며, 이들의 조합으로 최종 이미지의 각 픽셀 값이 결정된다.
Footprint function
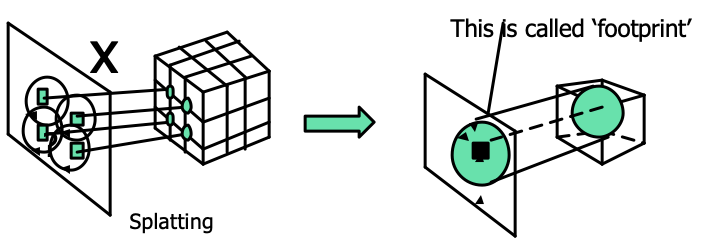
이제 footprint function 에 대해 알아보자.
footprint function이 필요한 이유는, 복셀 기여도를 정확하게 계산해야하기 때문이다. 또한 풋프린트 함수를 통해 각 스플랫이 지오메트리를 따르는 -안티앨리어싱에 기여할 수 있는- 형태로 유도할 수 있다.
이미지 평면 픽셀에 대한 복셀의 기여 식이 아래와 같이 복셀의 투영된 (x, y) 위치에만 의존하므로,
$$ I_s(p) = I_s(x, y) = \rho (s)\int_{-\infty }^{\infty}h_v(x-x_s, y-y_s, w)dw $$
이제 Footprint 함수를 다음과 같이 정의할 수 있다.
$$ footprint_s(x, y) = \int_{-\infty }^{\infty}h_v(x, y, w)dw $$
이 2D Shape 가 투영된 3D 커널이라는 것을 기억하면, 이제 (x, y)는 3D 커널의 투영 중심으로부터 (이미지 픽셀의) 변위를 나타내는 것을 알 수 있다.
Footprint Table
- 만일 우리가 균일한 그리드 간격을 가진 직각 좌표계 볼륨을 사용하고, 정사영 (orthographic projection) 을 수행한다면, 볼륨 내의 각 3D 커널 (Gaussians) 은 화면 상에서 동일한 투영을 가질 것이다. (단, 이미지 공간 offset은 제외.)
- 따라서, 우리는 '풋프린트 테이블'이라고 불리는 2D look-up table을 구축할 수 있다.
- 이 테이블은 화면상의 각 픽셀에 대해 스플랫이 그 픽셀에 얼마나 기여할지를 알려준다.
- 각 항목은 보통 0.0~1.0 사이의 값을 갖는다.
- 테이블은 스플랫의 중심을 중심으로 위치한다.
- 테이블의 크기는 이미지 해상도, 볼륨 크기 및 원하는 정확도에 따라 달라진다.
- 더 큰 테이블을 사용하면 더 큰 정확도를 달성할 수 있지만, 이미지 품질 측면에서는 비용이 발생할 수 있다.
Footprint Table 의 사용
- 볼륨 렌더링 과정에서 각 복셀을 순회하며 해당 복셀이 최종 이미지에 어떻게 기여하는지 파악할 때, 풋프린트 테이블을 accumulation sheet 위로 이동시키고, 그것을 accumulation sheet에 복사하는 것처럼 생각할 수 있음.
- 볼륨을 전면에서 후면으로, 한 층 (sheet)씩 순차로 통과하며 모든 풋프린트들을 accumulation sheet에 추가함.
- 그 후, accumulation sheet를 작업 중인 이미지와 합성함.
- 이를 통해 투영된 복셀들(스플랫)의 각 층이 최종 이미지에 영향을 미칠 수 있도록 보장함.
- 평행 투영(parallel projection)을 사용할 경우, 각 투영된 복셀의 범위(풋프린트)는 화면 공간상의 오프셋을 제외하고는 동일하다.
- 풋프린트를 사전에 계산하고, 각 스플랫에 대해 재사용할 수 있다.
- 그 다음 각 복셀에 대해, 스플랫이 화면상의 각 픽셀에 얼마나 그리고 어떻게 기여하는지를 다음과 같이 계산할 수 있다.$$ weight(x, y)_s = footprint(x-x_s, y-y_s) $$
- $ x_s, y_s $ 는 복셀 이미지 평면 투영을 나타내고, $ x, y $ 는 픽셀 이미지 평면 위치를 나타낸다.
- 테이블 자체는 3D 커널을 통해 선 적분(line integrals)을 수행함으로써 구축된다.
- 이는 3D 커널을 2D 시트에 투영하는 방법이며, 3D 밀도를 2D 이미지 평면에 어떻게 퍼뜨리거나 분배할지를 알려준다.
- 픽셀에 쓰여진 강도(intensity)는 복셀의 밀도 값에 따라 조절된다. $$ P(x, y) = weight(x, y)*\rho(s) $$
색상 할당
- Accumulation sheet는 각 픽셀마다 $ (R, G, B, \alpha) $ 튜플을 포함하게 된다.
- 그 후, 합성은 레이 캐스팅에서 사용되는 동일한 공식을 사용해 수행되지만, 여기선 픽셀단위로 일어난다.
- Splatting: 합성은 sheet를 따라 수행되며, 특정한 복셀 집합에 대해 한 번에 모든 픽셀에 대해 이뤄진다.
- Ray Casting: 합성은 레이를 따라 수행되며, 한 번에 하나의 보간된 데이터와 하나의 픽셀에 대해 이뤄진다.
- 수식으로 정리해보면 다음과 같다.
- 픽셀 p의 ray color에 대한 기여는: (F는 데이터의 밀도와 독립이다, F는 이미지에 대한 복셀의 기여도에 대한 가중치로 작동함.)$$ I_s(p) = \rho(s)F(x-x_s, y-y_s) $$
- 따라서 Total Contribution을 살펴보면, $ p\to (x, y) $ 의 ray color는: $$ I(p) = \int_{s}^{}I_s(p) = \int_{s}^{}\rho(s)F(x-x_s, y-y_s) $$
- 각 픽셀의 가중치는 서로 다른 샘플 s에 대한 footprint F로 주어진다.
- $ <x_s, y_s> $ 는 샘플 이미지 평면 투영을 나타내고 $ <x, y> $ 는 픽셀의 이미지 평면 위치를 나타냄.
- 즉 픽셀 $ p $ 에 대한 최종 이미지 색상 $ I(p) $ 는 모든 샘플 s에 대해 계산된 $ I_s(p) $ 의 합으로 구성된다.
- 각 샘플 $ s $ 에 대한 기여도 $ I_s(p) $ 는 샘플 $ s $ 의 밀도와 풋프린트 함수의 곱으로 계산된다.
- 여기서 F는 이미지 상의 픽셀 위치와 샘플 s의 이미지 평면 투영 위치 간의 상대적 위치에 따라 달라지는 풋프린트 함수의 가중치를 나타낸다.
- 이 과정에서 샘플 $ s $ 는 3D 볼륨 데이터 내의 복셀을 대표하며, 이 복셀의 밀도의 위치가 최종 이미지의 픽셀 값에 어떤 영향을 미칠지 결정한다. 스플래팅 기법은 이런 각 복셀의 기여도를 이미지 상의 픽셀들에 합산하여 최종 이미지를 생성하는 것이다.
-- 쓰는 중 --
'Computer Vision' 카테고리의 다른 글
| 대형차의 위험에 대비할 수 있도록 업데이트된 테슬라 FSD 11.4.9 (0) | 2024.02.14 |
|---|---|
| Convex Optimization 이란 무엇인가? (0) | 2024.01.20 |
| 3D Gaussian Splatting 이란 무엇인가? (0) | 2024.01.11 |
| Matrix Decomposition, 행렬 분해란 무엇인가? (1) | 2024.01.07 |
| 23.12.25 Daily Computer Vision Paper arXiv (0) | 2023.12.27 |

# 모바일에서 수식이 깨져보이니 PC모드 활용을 권장드립니다.
들어가며
컴퓨터 비전의 하위 도메인인 3D Reconstruction, Novel-View-Synthesis 을 공부하다보면 Volume Rendering, 혹은 그와 유사한 개념을 자주 접하게 된다.
하지만 렌더링에 사용되는 여러 개념을 혼동하거나 제대로 이해하지 못하는 경우가 많다.
특히 Splatting이 정확히 무엇인지에 대해서는 명쾌하게 답해주는 자료를 찾기 어려웠다.
각 개념을 이해해야 이후 Splatting, Ray Casting, 3D Gaussian splatting, NeRF 등에 잘 대응할 수 있으니 헷갈리는 부분을 짚고 넘어가려 한다.
이 글은 최초의 Splatting method 저자 Lee Alan Westover의 논문 "Alan, Lee. "SPLATTING: A Parallel, Feed-Forward Volume Rendering Algorithm." (1991)."를 참고했다.

Volume Rendering (볼륨 렌더링)
- 3D Volumetric data에서 직접 2D 이미지를 생성하는 기술
- 전체 3D 데이터를 2D 이미지로 매핑 함.
- 3D 데이터 내의 각 지점(복셀)에 대한 색상과 불투명도를 결정하여, 최종적으로 2D 이미지에 표현되는 시각적 효과를 결정
- 알고리즘 복잡성이 높고 시간이 오래 걸리지만 전체 정보를 유지함.
- 구름, 안개와 같은 비정형적 현상의 렌더링에 유리함.
- 2020년 ECCV에서 발표된 NeRF(Neural Radiance Fields)는 볼륨 렌더링을 미분가능한 방식으로 확장함.
Surface Rendering (표면 렌더링)
- 기하학적 기본 요소를 사용해 볼륨 데이터에 포함된 표면의 이미지를 생성하는 기술
- 기하학적 기본 형태는 주로 삼각형 또는 점이다.
- 볼륨 렌더링과는 다르게 표면에만 집중한다.
- 볼륨 데이터 내부의 구조보단 표면의 상세한 구조와 형태에 집중.
Clipping (클리핑)
- 렌더링 과정 중 볼륨의 일부를 제거하여 나머지 부분을 표시하는 과정.
- 불필요한 부분을 제거해 렌더링 효율성을 높일 수 있음.
- 볼륨 또는 표면 렌더링에 사용 가능함.
그렇다면 볼륨 렌더링을 구현하는 방법들에는 무엇이 있을까?
Object-order technique
- 볼륨 데이터가 이미지 평면에 매핑되는 포워드 매핑 체계를 사용함.
- -> Splatting (관련 논문: 3D Gaussian Splatting for Real-Time Radiance Field Rendering)
Image-order technique
- 이미지 평면의 각 픽셀에서 볼륨 데이터를 통해 광선을 캐스팅하여 픽셀 값을 결정하는 백워드 매핑 방식을 사용함.
- -> Volume Buffer, Ray Casting (관련 논문: Representing Scenes as Neural Radiance Fields for View Synthesis)
Hybrid technique
- 위의 두 방법을 융합
- -> Cell-by-cell V-buffer, Shear-warp
모든 방법들의 목표는 같다. 이미지를 만들어 내는 것이다.
즉 Splatting 이란 볼륨 렌더링 구현 방법 중, Object-order technique 방법에 속하는 알고리즘이다. (Proposed by Lee Westover, 1990)
그렇다면 Splatting 이란 정확히 무엇인가?
Splatting 은 각 샘플이 공간의 많은 점, 즉 이미지 평면의 많은 픽셀에 어떻게 기여할 수 있는지를 분포 함수의 관점에서 고려하는 알고리즘이다.
우선 Splatting 의 주요 개념과 단계를 알아보자.
- 에너지 분산(Distributing Energy): 입력 샘플들로부터 에너지를 공간에 분산시킴. 이는 각 샘플이 가지고 있는 정보(예: 밝기, 색상)를 공간의 여러 지점에 전달하는 과정을 의미함..
- 이미지 평면 발자국 계산(Calculating Image Plane Footprint): 각 데이터 샘플에 대한 '풋프린트' (Footprint)를 이미지 평면에서 계산함. 풋프린트는 해당 샘플이 이미지 평면에 어떻게 투영되는지를 나타내는 영역으로, 샘플의 에너지가 이미지 평면에 어떻게 분포될지를 결정함.
- 샘플의 에너지 분포(Spreading the Sample's Energy): 계산된 풋프린트를 사용하여 각 샘플의 에너지를 이미지 평면에 분산시킴. 이 과정에서 한 샘플이 이미지의 여러 픽셀에 영향을 줄 수 있으며, 이는 부드럽고 연속적인 시각적 효과를 생성함.
바로 이해하기 어려우므로 배경 개념부터 천천히 이해해보자.
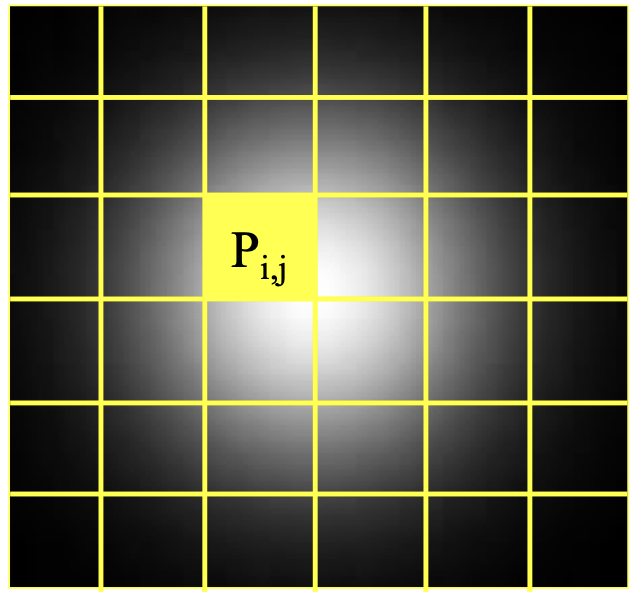
우선 픽셀을 샤프한 테두리를 가진 정사각형이 아닌, 아래 이미지처럼 흐릿한 경계를 가진 원형의 빛이라고 생각해보자.

Splatting 에서, 복셀도 같은 방식으로 여겨진다.
Descrete point 가 아닌, 가우시안 분포를 나타내는 흐릿한 구형으로 말이다.
(이 3D 가우시간은 'Reconstruction Kernel' 로 불린다.)
따라서 우리는 볼륨을 불연속적인 물체가 아닌 연속적인 함수(Gaussians)의 집합으로 정의되는 연속적인 물체로 생각할 수 있다.
그리고 각 가우시안의 중심에 복셀의 밀도를 지정한다.
중심에서 멀어질 수록 밀도는 가우시안 분포에 의해 빠르게 떨어진다.
일반적으로 μ = 0.0, σ = 1.0, 피크값=1.0 을 사용하며 반경 2.0 바깥의 값은 잘라낸다. 즉 그 바깥 영역의 밀도는 0이다.
(물론 위와 같은 표준 정규분포에서 피크값이 1.0이 나올 순 없다. 시각적 표현을 위해 조정한 분포를 사용한다.)

이제 3D 커널과 그것의 2D 스플랫이 어떻게 작동하는지 알아보자.
3D 커널과 2D 스플랫은 서로 오버랩된다.
앞서 말했듯, 3D 커널은 볼륨 데이터 내의 각 점(복셀) 주위에 분포하는 값을 정의하는 함수다. 2D 스플랫은 이 커널이 2차원 이미지 평면에 투영되었을 때의 형태다. 이 스플랫들은 서로 오버랩되어 이미지 평면에 분포한다.
스플랫들이 오버랩되는 것이 중요한 이유는 그렇게 함으로써 다양한 카메라 포즈가 달라지거나 줌인/줌아웃(스케일링)을 하더라도 일관되며 연속적이고 부드러운 이미지를 볼 수 있기 때문이다.
*카메라의 줌인/줌아웃 시 2D 스플랫은 시각적 일관성을 위해 크기가 조절된다.

이제 Splatting 알고리즘 개요를 알아보자.


알고리즘은 변환, 음영, 재구성, 가시성 처리를 통해 최종 2D 이미지를 제작한다.
3D 볼륨 데이터는 복셀의 격자로 구성되어 있다.
1. 알고리즘은 볼륨을 Sheet(시트) 라고 불리는 한 겹씩 순차적으로 처리한다. 이때, 시트는 복셀의 층을 의미한다.
2. 처리할 시트를 선택할 때, 이미지 평면과 가장 평행한 시트(x-y, x-z, y-z)를 선택한다. (렌더링 효율성을 위해)
3. 선택한 시트의 각 복셀은 (i, j, k) 그리드 공간에서 (x, y, z) 스크린 공간으로 변환된다.
이 변환에는 translation, rotation이 동반될 수 있다.
이 과정에서 3D -> 2D 평면 매핑이 이뤄진다.
4. 변환된 각 복셀은 색상(RGB)와 투명도(alpha)를 갖도록 음영처리된다. (Shaded)
여기서 Shading rule이 사용된다. <x,y,z,R,G,B,A>.
여기서 가시성(Visibility) 처리가 이뤄진다.
5. 누적 시트에 대한 복셀의 영향 결정 (재구성 단계)
각 복셀이 누적 시트(Accumulation sheet)에 어떤 영향을 미칠지 결정한다.
이는 각 복셀을 누적 시트에 projection하는 과정을 통해 이뤄진다.
이를 위해 풋프린트 함수 (footprint function)을 정의하고 계산된다.
데이터 샘플은 재구성 커널(reconstruction kernel)과 합성되어(data sample이 convolved with), 이 샘플의 이미지를 생성한다.
-> 앞에 설명한 3D 가우시안이 재구성 커널임. 3D 가우시안, 재구성 커널은 복셀의 데이터값을 주변 공간에 어떻게 확산시킬지를 정의하는 함수이다.
6. 시트처리 후 누적 시트와 작업 이미지의 결합 (가시성 처리)
한 시트의 모든 복셀이 처리되면, 누적 시트는 중간 단계의 작업 이미지와 결합된다.
이 과정에서 합성 연산자(Composition operator)를 사용함.
7. 모든 시트 처리 후 최종 이미지 생성
복셀의 이미지 평면에 대한 기여
1. 투영된 3D 가우시안 커널의 2D 영역
3D 공간에서 정의된 가우시안 커널 (함수)이 2D 이미지 평면에 투영될 때의 영역을 '스플랫' 혹은 '풋프린트'라 한다.
2. 데이터셋을 연속 함수로 생각하기
데이터셋은 부드러운 가우시안 커널 (함수)에 의해 조각별로 정의된 연속함수로 정의된다. 각 복셀은 이 연속함수의 일부를 형성한다.
3. 볼륨에 대한 복셀의 기여 (Contribute)
볼륨에 대한 복셀의 기여는 다음과 같은 식으로 표현된다.
$$ contribution_s(x,y,z) = h_v(x-x_s, y-y_s, z-z_s)\rho (s) $$
여기서, $ h_v $ 는 볼류메트릭 재구성 커널이고, $ \rho (s) $ 는 복셀의 밀도를 나타낸다.
즉, 복셀의 밀도가 클 수록 볼륨 더 많은 기여를 한다. (NeRF의 opacity를 떠올리게 함.)
이처럼 복셀의 데이터값이 주변 공간에 확산되는 과정은 재구성 커널과 복셀 밀도의 곱으로 계산된다.
이를 다시 말해 '볼륨에 대한 복셀의 기여'라고 한다.
참고로, 복셀의 밀도 $ \rho (s) $ 는 $ \rho (s) = \rho (x_s, y_s, z_s) $ 로 정의된다.
4. 이미지 평면 픽셀에 대한 복셀의 기여 (Contribute)
복셀 데이터 샘플 $ s $ 가 이미지 평면 픽셀 $ p \to (x, y) $ 에 미치는 기여는 아래 식으로 표현된다.
$$ I_s(p) = I_s(x, y) = \rho (s)\int_{-\infty }^{\infty}h_v(x-x_s, y-y_s, w)dw $$
여기서 $ w $ 는 스크린에 수직인 광선 (네거티브 z축, pointing into the screen)을 따라 계산되며 그 원점은 $ (x, y) $ 이다.
또한 주어진 복셀에 대해, $ \rho (s) $ 는 $ \rho $ 가 w에 독립적이므로 일정하다.
때문에, 밀도항을 적분 밖으로 옮길 수 있다.
다시 한 번, 적분은 복셀의 밀도에 독립적이라는 점에 유의해야 한다.
5. $ x_s, y_s, z_s $
복셀의 위치를 나타내는 3차원 공간 상의 좌표
6. $ x, y, z $
카메라 기준의 3차원 공간 상의 좌표. 즉 볼륨 데이터가 projection 되어야 하는 이미지 평면의 위치를 나타냄.
7. 재구성 커널 h의 의미
$$ h_v(x-x_s, y-y_s, z-z_s) $$
이 커널(함수)는 중심점에서 멀어질수록 값이 감소하는 형태를 갖는다.
복셀의 3차원 상 좌표 $ x_s, y_s, z_s $ 에서 이미지 평면 상의 관찰점 $ x, y, z $ 까지의 거리에 따라 복셀이 갖는 영향력을 나타내는 것이다.
즉 복셀의 중심으로부터 멀어질수록 영향력은 감소하며, 이를 통해 볼륨 데이터의 부드러운 그라데이션을 확보한다.


위 그림처럼 복셀의 중심은 해당 복셀이 가진 데이터 값(예: 밀도, 색상)의 영향을 가장 강하게 받기 때문이다.
따라서 결과값은 입력값의 가중평균이다.
여기서 포워드 매핑 vs. 백워드 매핑의 차이가 드러난다.
포워드 매핑 (Splatting)
- 포워드 매핑 방식에서의 컨볼루션은 입력이 출력에 에너지를 분배하여 출력을 생성하는 것으로 본다.
- 여기서 스플래팅 방식은 각 입력 포인트(복셀)가 이미지 평면의 여러 픽셀에 영향을 미치는 것을 의미한다
- 즉, 하나의 입력이 여러 출력 픽셀에 '에너지'를 분배함으로써 최종 이미지가 형성된다.
백워드 매핑 (Ray Casting)
- 백워드 매핑 방식에서의 컨볼루션은 출력을 입력의 가중 평균으로 생성하는 것으로 간주한다.
- 즉, 각 입력 포인트(예: 복셀)의 기여도가 가중치에 따라 계산되며, 이들의 조합으로 최종 이미지의 각 픽셀 값이 결정된다.

Footprint function

이제 footprint function 에 대해 알아보자.
footprint function이 필요한 이유는, 복셀 기여도를 정확하게 계산해야하기 때문이다. 또한 풋프린트 함수를 통해 각 스플랫이 지오메트리를 따르는 -안티앨리어싱에 기여할 수 있는- 형태로 유도할 수 있다.
이미지 평면 픽셀에 대한 복셀의 기여 식이 아래와 같이 복셀의 투영된 (x, y) 위치에만 의존하므로,
$$ I_s(p) = I_s(x, y) = \rho (s)\int_{-\infty }^{\infty}h_v(x-x_s, y-y_s, w)dw $$
이제 Footprint 함수를 다음과 같이 정의할 수 있다.
$$ footprint_s(x, y) = \int_{-\infty }^{\infty}h_v(x, y, w)dw $$
이 2D Shape 가 투영된 3D 커널이라는 것을 기억하면, 이제 (x, y)는 3D 커널의 투영 중심으로부터 (이미지 픽셀의) 변위를 나타내는 것을 알 수 있다.
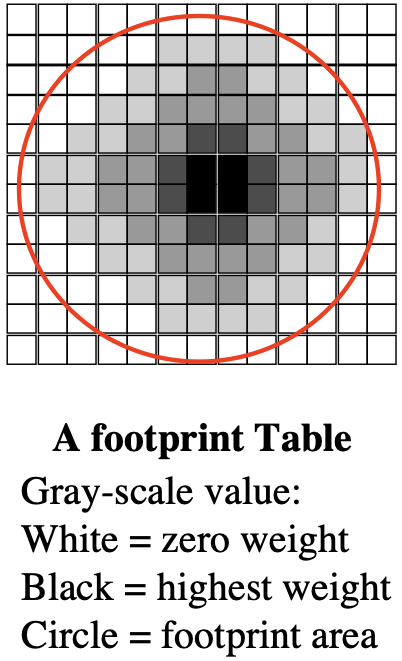
Footprint Table
- 만일 우리가 균일한 그리드 간격을 가진 직각 좌표계 볼륨을 사용하고, 정사영 (orthographic projection) 을 수행한다면, 볼륨 내의 각 3D 커널 (Gaussians) 은 화면 상에서 동일한 투영을 가질 것이다. (단, 이미지 공간 offset은 제외.)
- 따라서, 우리는 '풋프린트 테이블'이라고 불리는 2D look-up table을 구축할 수 있다.
- 이 테이블은 화면상의 각 픽셀에 대해 스플랫이 그 픽셀에 얼마나 기여할지를 알려준다.
- 각 항목은 보통 0.0~1.0 사이의 값을 갖는다.
- 테이블은 스플랫의 중심을 중심으로 위치한다.
- 테이블의 크기는 이미지 해상도, 볼륨 크기 및 원하는 정확도에 따라 달라진다.
- 더 큰 테이블을 사용하면 더 큰 정확도를 달성할 수 있지만, 이미지 품질 측면에서는 비용이 발생할 수 있다.


Footprint Table 의 사용
- 볼륨 렌더링 과정에서 각 복셀을 순회하며 해당 복셀이 최종 이미지에 어떻게 기여하는지 파악할 때, 풋프린트 테이블을 accumulation sheet 위로 이동시키고, 그것을 accumulation sheet에 복사하는 것처럼 생각할 수 있음.
- 볼륨을 전면에서 후면으로, 한 층 (sheet)씩 순차로 통과하며 모든 풋프린트들을 accumulation sheet에 추가함.
- 그 후, accumulation sheet를 작업 중인 이미지와 합성함.
- 이를 통해 투영된 복셀들(스플랫)의 각 층이 최종 이미지에 영향을 미칠 수 있도록 보장함.
- 평행 투영(parallel projection)을 사용할 경우, 각 투영된 복셀의 범위(풋프린트)는 화면 공간상의 오프셋을 제외하고는 동일하다.
- 풋프린트를 사전에 계산하고, 각 스플랫에 대해 재사용할 수 있다.
- 그 다음 각 복셀에 대해, 스플랫이 화면상의 각 픽셀에 얼마나 그리고 어떻게 기여하는지를 다음과 같이 계산할 수 있다.$$ weight(x, y)_s = footprint(x-x_s, y-y_s) $$
- $ x_s, y_s $ 는 복셀 이미지 평면 투영을 나타내고, $ x, y $ 는 픽셀 이미지 평면 위치를 나타낸다.
- 테이블 자체는 3D 커널을 통해 선 적분(line integrals)을 수행함으로써 구축된다.
- 이는 3D 커널을 2D 시트에 투영하는 방법이며, 3D 밀도를 2D 이미지 평면에 어떻게 퍼뜨리거나 분배할지를 알려준다.
- 픽셀에 쓰여진 강도(intensity)는 복셀의 밀도 값에 따라 조절된다. $$ P(x, y) = weight(x, y)*\rho(s) $$
색상 할당
- Accumulation sheet는 각 픽셀마다 $ (R, G, B, \alpha) $ 튜플을 포함하게 된다.
- 그 후, 합성은 레이 캐스팅에서 사용되는 동일한 공식을 사용해 수행되지만, 여기선 픽셀단위로 일어난다.
- Splatting: 합성은 sheet를 따라 수행되며, 특정한 복셀 집합에 대해 한 번에 모든 픽셀에 대해 이뤄진다.
- Ray Casting: 합성은 레이를 따라 수행되며, 한 번에 하나의 보간된 데이터와 하나의 픽셀에 대해 이뤄진다.
- 수식으로 정리해보면 다음과 같다.
- 픽셀 p의 ray color에 대한 기여는: (F는 데이터의 밀도와 독립이다, F는 이미지에 대한 복셀의 기여도에 대한 가중치로 작동함.)$$ I_s(p) = \rho(s)F(x-x_s, y-y_s) $$
- 따라서 Total Contribution을 살펴보면, $ p\to (x, y) $ 의 ray color는: $$ I(p) = \int_{s}^{}I_s(p) = \int_{s}^{}\rho(s)F(x-x_s, y-y_s) $$
- 각 픽셀의 가중치는 서로 다른 샘플 s에 대한 footprint F로 주어진다.
- $ <x_s, y_s> $ 는 샘플 이미지 평면 투영을 나타내고 $ <x, y> $ 는 픽셀의 이미지 평면 위치를 나타냄.
- 즉 픽셀 $ p $ 에 대한 최종 이미지 색상 $ I(p) $ 는 모든 샘플 s에 대해 계산된 $ I_s(p) $ 의 합으로 구성된다.
- 각 샘플 $ s $ 에 대한 기여도 $ I_s(p) $ 는 샘플 $ s $ 의 밀도와 풋프린트 함수의 곱으로 계산된다.
- 여기서 F는 이미지 상의 픽셀 위치와 샘플 s의 이미지 평면 투영 위치 간의 상대적 위치에 따라 달라지는 풋프린트 함수의 가중치를 나타낸다.
- 이 과정에서 샘플 $ s $ 는 3D 볼륨 데이터 내의 복셀을 대표하며, 이 복셀의 밀도의 위치가 최종 이미지의 픽셀 값에 어떤 영향을 미칠지 결정한다. 스플래팅 기법은 이런 각 복셀의 기여도를 이미지 상의 픽셀들에 합산하여 최종 이미지를 생성하는 것이다.
-- 쓰는 중 --
'Computer Vision' 카테고리의 다른 글
| 대형차의 위험에 대비할 수 있도록 업데이트된 테슬라 FSD 11.4.9 (0) | 2024.02.14 |
|---|---|
| Convex Optimization 이란 무엇인가? (0) | 2024.01.20 |
| 3D Gaussian Splatting 이란 무엇인가? (0) | 2024.01.11 |
| Matrix Decomposition, 행렬 분해란 무엇인가? (1) | 2024.01.07 |
| 23.12.25 Daily Computer Vision Paper arXiv (0) | 2023.12.27 |
